●はじめに
鏡はなぜ左右対称に映るのか。自分も以前考えたことがあっていつかブログに書こうと思っていたのですが、NHKの番組「チコちゃんに叱られる!」で取り上げたとのことで、それをまとめたサイトを見たところ「人それぞれで捉え方が違うためわからない」とのことでした。番組自体は見てません。でも、この際なので自分なりに考え直してまとめてみました。あと、英訳しました。
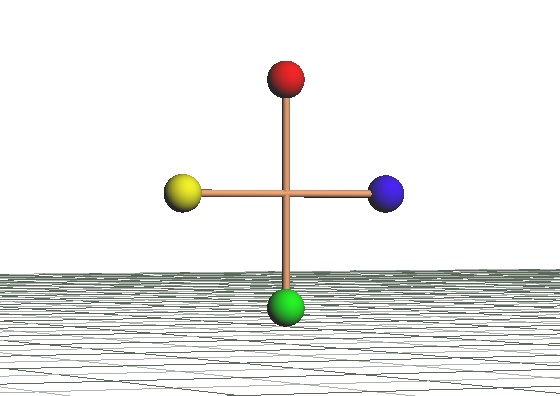
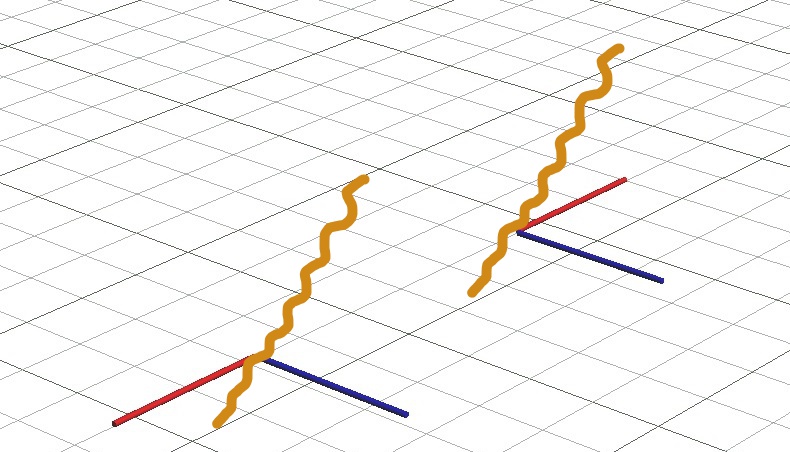
魚の方は手前が左で奥が右、とすぐわかります。でも、隣のロケットの左右は……と言われても、ちょっと困るのではないでしょうか。次のイラストを見て下さい。イソギンチャクと、イソギンチャクを付けた貝を背負っているヤドカリです。
イソギンチャクの左右は……と言われても戸惑うでしょう。でも、ヤドカリに背負われたほうはなんとなく言わんとしていることを勘案して答えられそうです。
魚とロケットの前後方向はわかりますが上下が明確なのは魚のほうだけです。また、イソギンチャクとそれを背負ったヤドカリの上下はわかりますが、前後方向が明確なのはヤドカリがいるほうです。これより、前後だけ、あるいは上下だけしかわかってないと左右を決めるのは困難であり、前後と上下が判明した場合にやっと左右が決定できることがわかります。
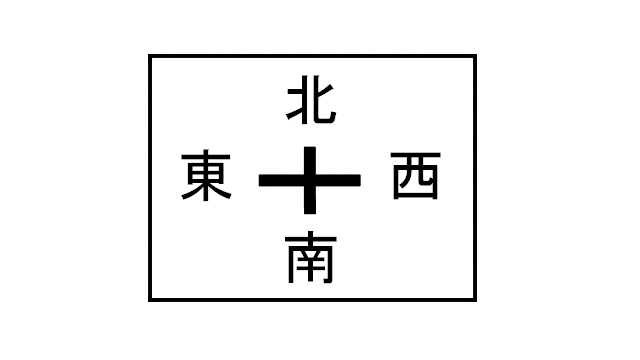
ここで方位についても触れておきます。南を向けば自動的に右手が西、左手が東になると思われている方もいるのではないでしょうか。では、まず下の図を見て下さい。
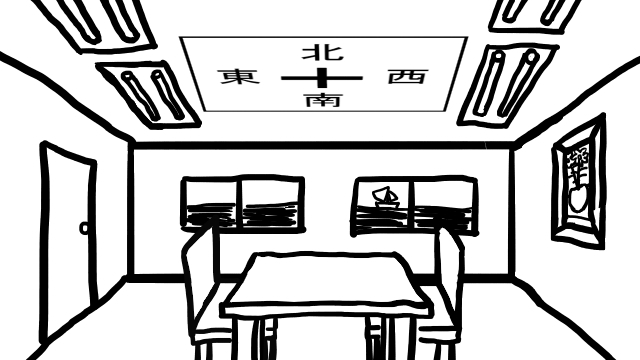
東西が逆になった方位図です。こんなの使いようがないって?それが、使えるのですね。次のイラストのように。
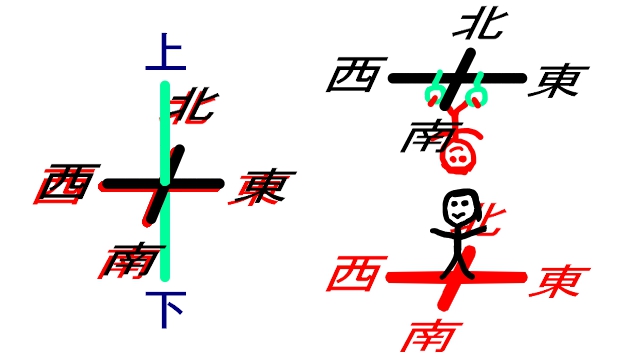
天井に貼れば正しい方位を指すので使えます。つまり、普段は意識してませんが、方位も以下の図のように上下方向抜きでは正しく使うことができないということです。
下の人にとっては、南を向けば右手が西、左手が東です。でも上の上下逆さまの人からみると、南を向けば左手が西、右手が東ですね。
●「鏡に左右逆に映る」とは?
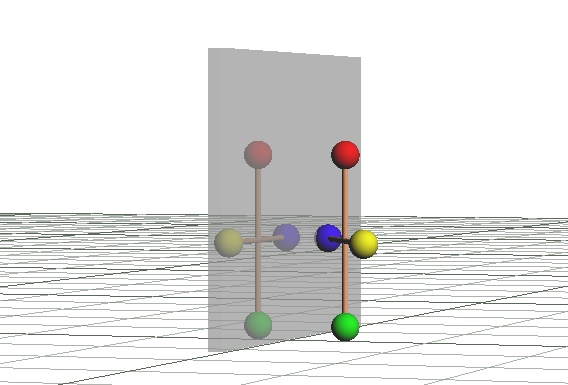
さて、ここからが本題です。ハニワが図のように鏡に映ったとしましょう。
そして、鏡に映ったハニワが飛び出て来たとします。
この二つのハニワを比べるとき、私たちは普通このように並べて比べているのではないでしょうか。
そう、つまり
1. 上下方向をそろえる
2. 前後をそろえる
3. 左右を比べる
たいていこの順番のはずです。なので、この場合鏡に映ったものは左右逆と認識することになります。いや、もう少し正確に書くなら「鏡に映ったものは左右だけ逆」でしょうか。ここで「逆」とは物体の中心に対して他の物体と別の側にあることを意味します。しかし。このように並べてみたらどうでしょうか。
上下方向と左右方向をそろえてみました。ここで「そろえる」とは物体の中心に対して他の物体と同じ側にすることだといえます。先に述べた「逆」の逆ですね。ハニワの「中央に対して腕を上げたほう」の左右方向をそろえたのですが、この場合、「左右(をそろえてみました。)」と書くと「右手(右腕)」や「左手(左腕)」のような、「普通に立っている状態を前提として名付けられた体の特定の部位の名称」を意識してしまうので「左右方向」と書きました。あくまでも「ハニワの中心に対しての位置」に注目してほしかったからです。わかってください。さて、こう並べた場合は見ての通り前後逆です。つまり、「鏡に映ったものは前後だけ逆」ですね。
なお、先の「チコちゃんに叱られる!」では運転中にバックミラーに映った自分を追い越す車を見るときは左右逆を意識していないという話があったようですが、車が右側から追い抜かれるとき、鏡の中の車は左から追い抜かれることに注意してください。
これも、上下の次に左右を、「逆」ではなく、「そろえる」ことを意識した例といえるでしょう。
さらに、左右・前後とくれば上下についても確認する必要があります。
前後方向と左右方向をそろえてみました。この場合、「鏡に映ったものは上下だけ逆」になったわけです。間違ってないですよね。
ここまでの話をまとめてみます。鏡に映った物体と元の物体を比べた場合、
・上下方向と前後方向をそろえると、左右方向だけが逆になる
・上下方向と左右方向をそろえると、前後方向だけが逆になる
・前後方向と左右方向をそろえると、上下方向だけが逆になる
ということがいえます。
●方向の名称について
さて。前章では上下方向・前後方向・左右方向の三つの組について考えてきましたが、改めてそれらの名称の必然性について考えてみます。
まず、上下方向は重力の向きによって決まりますが、前章では重力の話はしませんでした。また、本記事の最初に取り上げた魚にしろヤドカリにしろ、上下方向に対して垂直方向に物体が進む方向を「前」としてきましたが、前章ではハニワは移動していません。「前」から上下方向に対して垂直方向の物体の反対側が「後」です。そして、上下方向と前後方向に対して垂直方向にあるのが「右」と「左」です。「上」「下」と銘打っているのに重力の話をせず、「前」と「後」も移動方向を意味せず物体の側面の名称にすぎないのなら、「右」と「左」も「前」「後」と同じく側面の位置を示す名称以上の意味はありません。
これより、上下方向・前後方向・左右方向の名称のいずれも「他の二方向に対して垂直方向に存在する」程度の意味しかないといえます。よって、鏡に映った物体の話をする際にはこれらを仮にa1a2方向・b1b2方向・c1c2方向という名前にしても差し支えないでしょう。
●鏡の性質について
鏡の性質を再確認するために以下のようなものを考えてみます。
この物体を、鏡に映すと次のようになります。
鏡は光を跳ね返す物体です。もう少し詳しく言うなら、鏡の面に対して垂直に当たった光を垂直に跳ね返す性質があります。その結果、「物体の鏡の面に平行な断面」とそれが鏡に映った像(鏡像)は、それらを元の光の光源の側から見るなら同じになります。
しかし、実際にここで扱うのは断面ではなく立体です。着目するのは鏡の面と「元の物体の鏡に面した方」からの視点であり、この場合、元の物体のその断面を元の光の光源の反対側から見ることになります。
つまり、物体とその鏡像について、その鏡の面に対して垂直な方向、すなわち前後方向については逆向きになります。あるいは、鏡はその性質上、元の物体をその面に垂直な一方向について変換して逆となる鏡像をつくる、ともいえます。
●鏡像の三方向の考察 その1
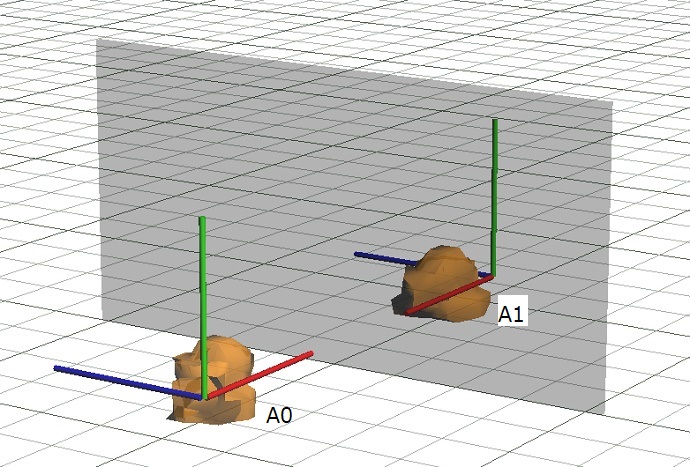
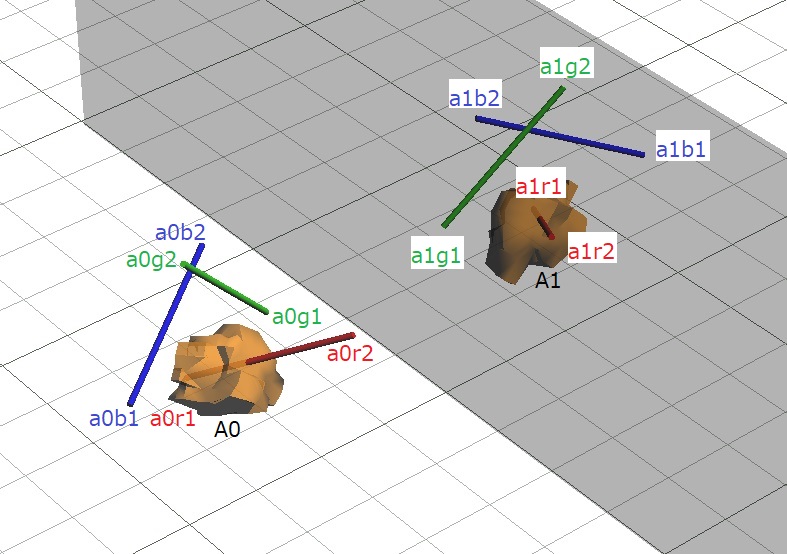
まず、改めてある三次元の物体A0とその鏡像A1を考えてみます。
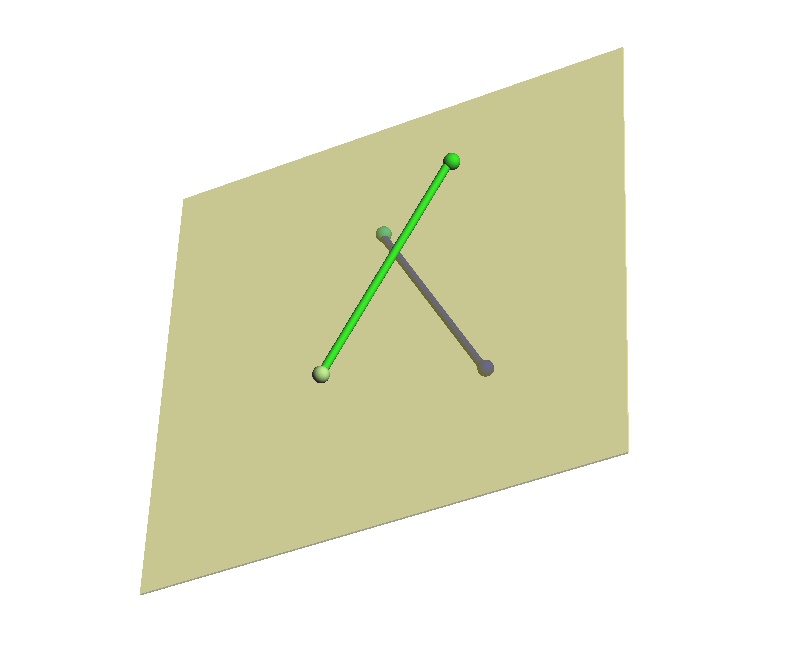
この鏡像A1は「元の物体の『鏡に平行で互いに垂直な二方向(青、緑)』はそろっているが、鏡に垂直な一方向(赤)については逆の物体」とも言えます。では、物体A0と鏡像A1について、この三方向以外のあらゆる三方向についても同じことが言えるか、つまり、物体A0の任意の互いに垂直な三方向のうち二方向を鏡に平行にした場合、残り一方向について物体A0と鏡像A1は逆であるといえるのか検討してみます。物体A0に、先の三方向と異なる互いに垂直な三方向を定めたとします。
この場合、そのうちの二方向を鏡に平行になるように物体A0を回転すると残りの一方向は鏡に垂直になります。
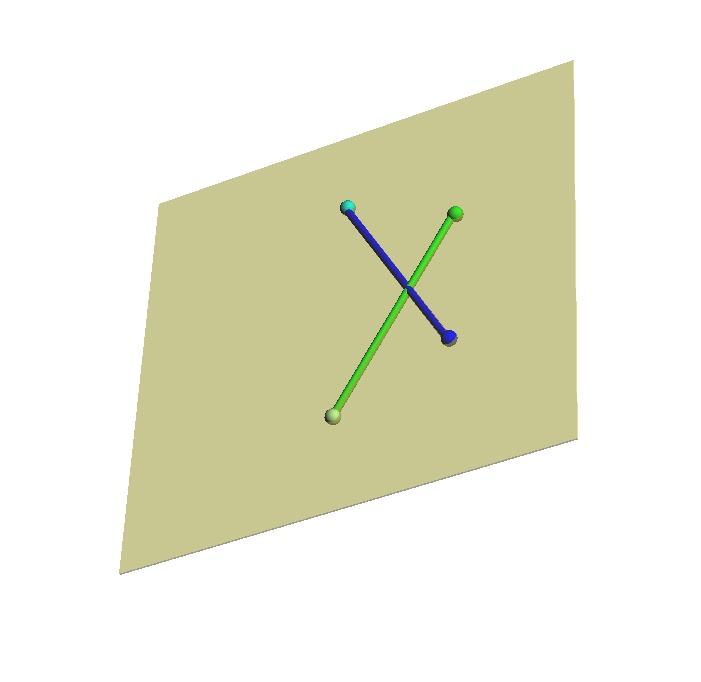
このときの物体A0の鏡像を鏡像A2とすると、鏡像A2は鏡像A1を回転させたものといえるので同じ物体といえます。よって、互いに垂直な三方向を任意に定めたある物体とその鏡像について、元の物体とその鏡像の二方向をそろえた場合、残りの一方向は逆になるといえます。
これでいいと思うのですが……だめだ、なんか納得できない。直感というか現象として納得しても理屈として納得できないというか。「確かにそうなる」のだろうけど「なぜそうなる」のかには答えきれていないような。
物体A0についてある一方向についてのみ逆にしただけなのに、なぜ他の方向についても同様に、物体と鏡像の二方向をそろえたら他の一方向が逆になる現象が同等に生じるのか。おそらく、鏡像A2は鏡像A1と本当に同じ物体なのか、これだけでは書ききれてないからなんだろうな。これを自明と言えたらどんなに楽なことか。一般常識的にいえば自明なのですけどね。もしかしたら、鏡像A1を鏡像A2に回転する際に少しずつ何らかの変形がされているのかもしれない。そして、仮に鏡像A2と鏡像A1が別の物体であったとしてもこれでは見過ごされそうというか、そんな感覚が残ります。
●向きと二方向に平行な平面の話
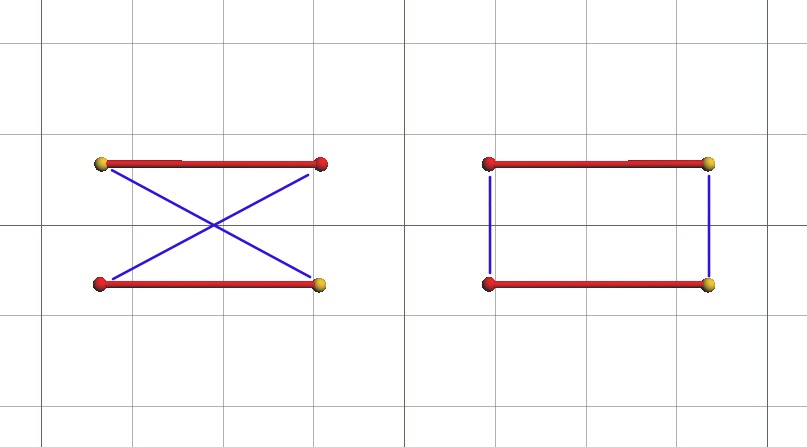
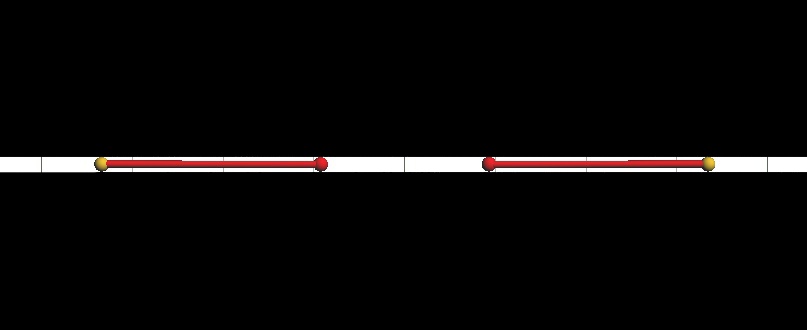
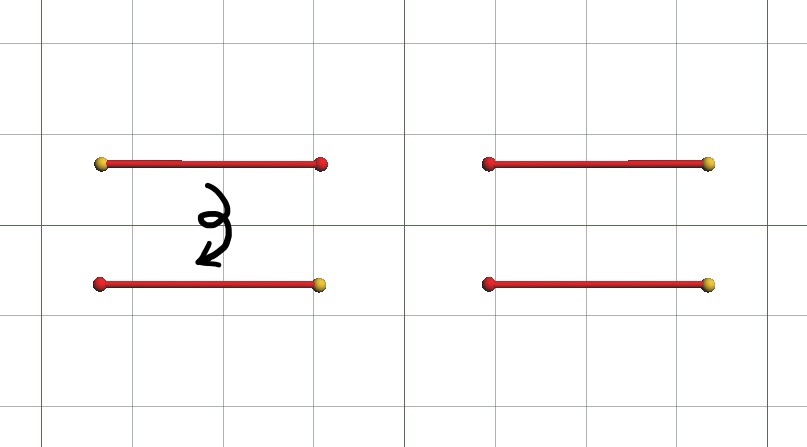
まず、方向とはどんなものか再確認します。方向とは「一直線」で「向きがあるもの」ですよね。そして「(二方向の)方向をそろえる」とは、1.二つの直線を平行にする、2.向きを一致する、の二つの要素からなっています。2.をもう少し数学っぽく言うなら「1.の状態で二つの軸の同じ向きを直線で結んだときに交点ができない」とでも言えばいいのでしょうか。
左がそろっていない例、右がそろっている例です。
次に、「二方向」について考えてみます。互いに平行でない二つの方向については、ただ一つ……ではなく、ただ一方向だけ、この二つの方向に対して交わらない平面が決まります。
一方向に対してはこの方向に対して交わらない向きの平面がたくさん決められますが、この方向に対して平行でない方向が定まると、それによって平面の向きが定まるイメージです。あるいは、この二方向を平行移動してある点で重なったときに、その二方向を含む平面が存在するような。これは、この二方向が平行でさえなければ、互いに垂直でなくても通じる話です。
この平面を使って話を進めます。
●鏡像の三方向の考察 その2
改めて、ある物体とその鏡像(ある一方向の座標だけ逆にした物体)の任意の二方向をそろえた場合、残りの一方向(先の逆にした方向とは必ずしも一致しない)については逆になることを証明したいと思います。物体とその鏡像のそれぞれの任意の二方向をそろえたとき、その二方向に平行な平面同士も平行になり、このとき物体上の点とその鏡像はそれらの平面の垂直方向、すなわち残りの一方向に対して逆になる、というのが全体のおおまかな流れです。
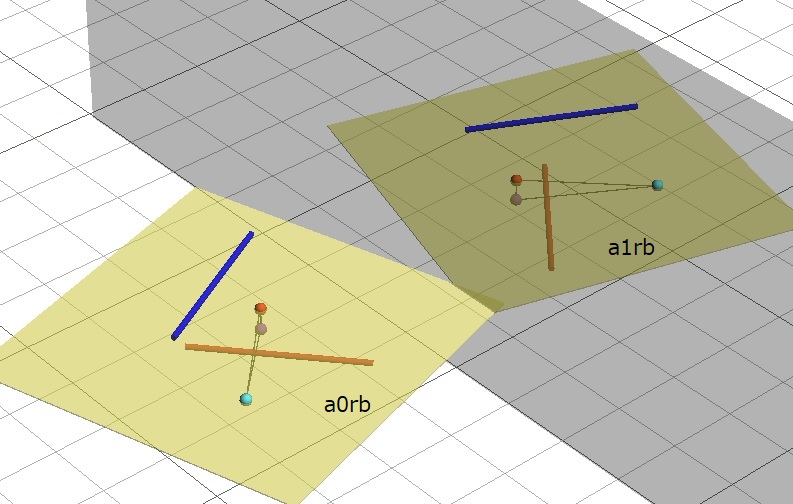
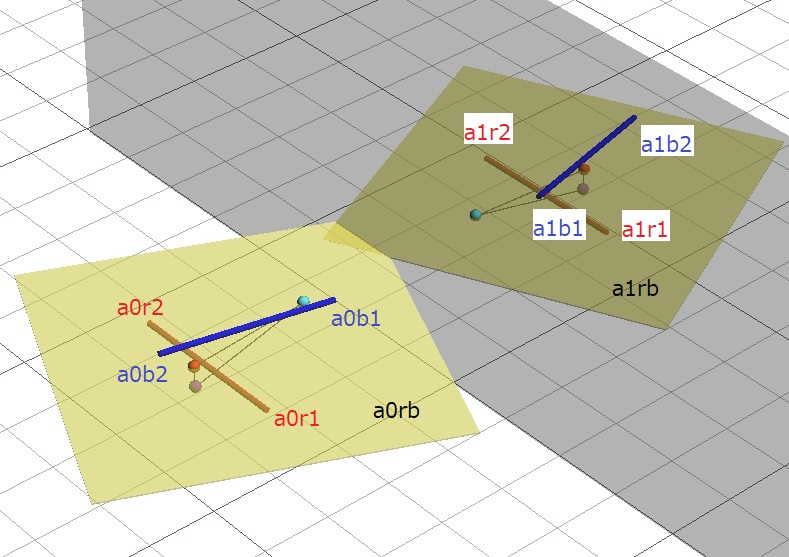
物体A0と鏡像A1について、A0の任意の互いに平行でない三方向(鏡に対して平行でも垂直でもないものとする。)a0r1-a0r2、a0b1-a0b2、a0g1-a0g2があったとします。このうちa0r1-a0r2、a0b1-a0b2の二方向の鏡像をa1r1-a1r2、a1b1-a1b2とします。
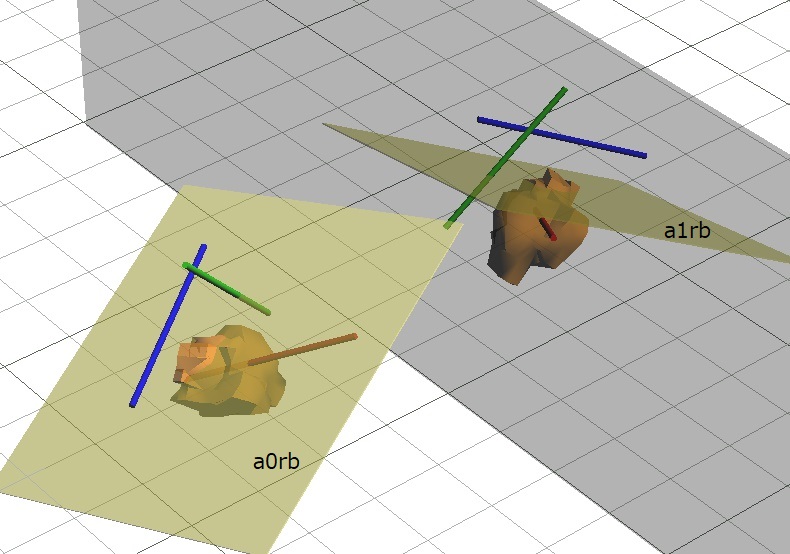
また、a0r1-a0r2、a0b1-a0b2に対して平行な面を面a0rb、その鏡像を面a1rbとします。言うまでも無く面a1rbはa1r1-a1r2、a1b1-a1b2の二方向に対して平行です。
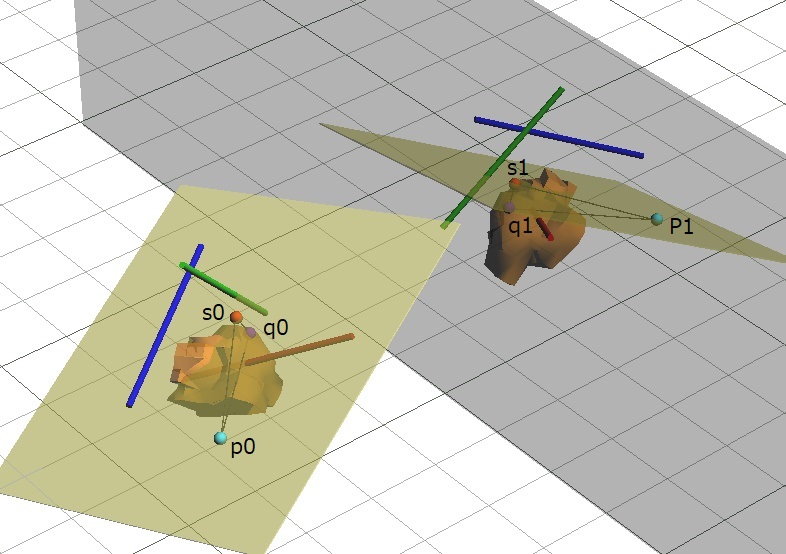
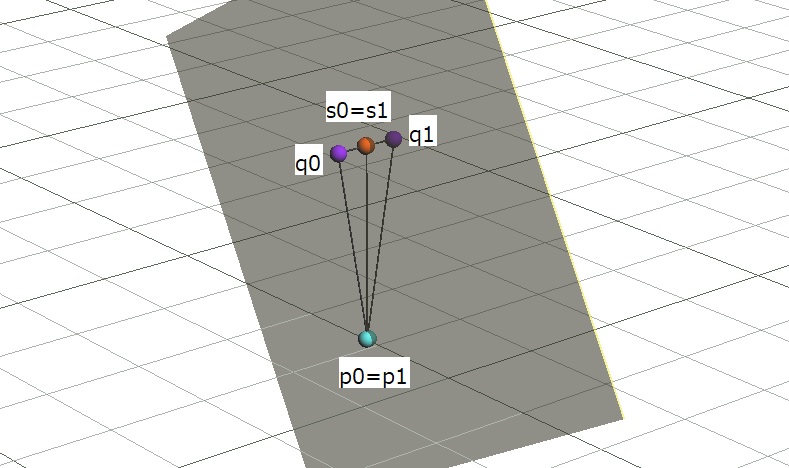
また、面a0rb上の任意の点p0、その鏡像をp1とします。p1は面a1rb上にあります。物体A0上の点をq0、その鏡像をq1とします。q1は鏡像A1上にあります。また、点q0を通る面a0rbに垂直な線と面a0rbとの交点をs0、その鏡像をs1としたとき、点s1は平面a1rb上にあり、また、このとき三角形p1q1s1は三角形p0q0s0の鏡像ともいえるので合同です。
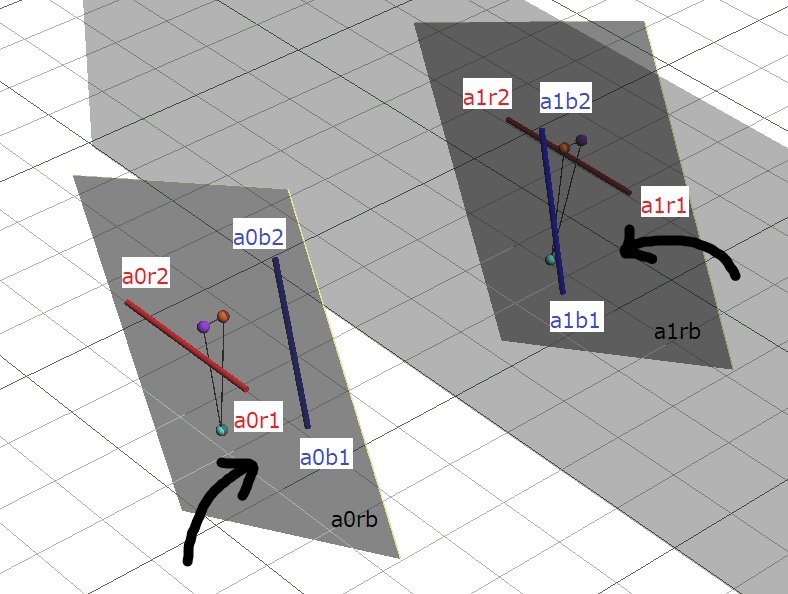
ここで、「物体A0のa0r1-a0r2、a0b1-a0b2の二方向と物体A1のa1r1-a1r2、a1b1-a1b2の二方向をそろえる」ことを考えてみます。このときa0r1-a0r2、a0b1-a0b2に合わせて面a0rb、点p0、q0、s0を、またa1r1-a1r2、a1b1-a1b2に合わせて面a1rb、点p1、q1、s1を一緒に空間的位置関係を保ったまま移動すると、以下の図のようになります。
面a0rbはa0r1-a0r2、a0b1-a0b2と平行なので、それと平行なa1r1-a1r2、a1b1-a1b2とも交わりません。同様に、面a1rbはa0r1-a0r2、a0b1-a0b2と交わりません。よって、a0r1-a0r2、a0b1-a0b2と平行になる平面の向きは一つであり、a1r1-a1r2、a1b1-a1b2と平行になる平面の向きも一つであるので、平面a0rbと平面a1rbは同じ向きであり、すなわち平行であるといえます。
●物体上と鏡像上の点と平面について
次に、このとき点q0、q1が面a0rb、a1rbに対して逆方向にあることを説明します。先の物体A0と鏡像A1の二方向をそろえる動作を、各要素を同時に鏡の面に対して対称に移動することができれば、各要素は初期状態で鏡の面に対して対称であり、対称移動しかしていない以上移動後も各要素は鏡の面に対して対称で、そして移動後は面a0rb、a1rbは鏡の面と平行なので、点q1、面a1rbは点q0、面a0rbの鏡像であり、これは鏡の面、面a0rb、a1rbの垂直方向については逆であるといえる、というのがこの章の大まかな流れです。
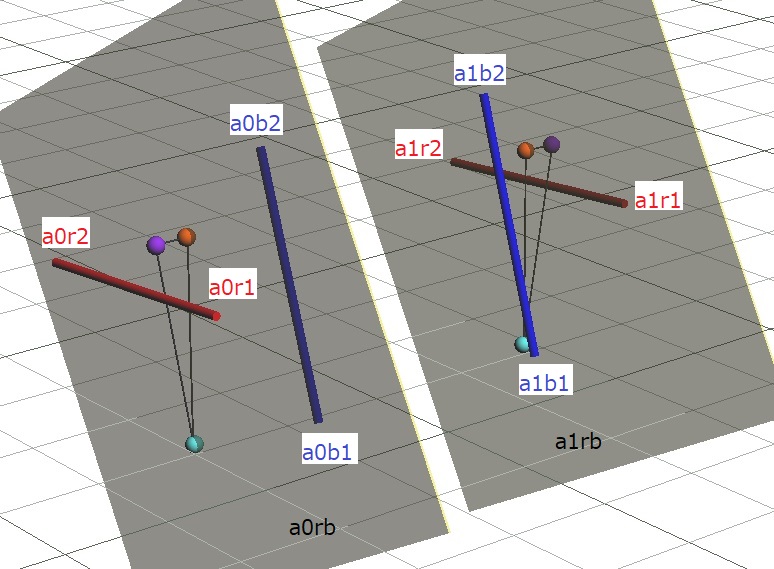
まず、面a0rb、a1rbを鏡の面に対して垂直な位置になるように回転移動します。面a0rbに合わせて、a0r1-a0r2、a0b1-a0b2、点p0、q0、s0を、また面a1rbに合わせてa1r1-a1r2、a1b1-a1b2、点p1、q1、s1を一緒に空間的位置関係を保ったまま移動すると、以下の図のようになります。
このとき、面a0rb、a1rbとa0r1-a0r2、a1r1-a1r2は移動前から鏡の面に対して対称であり、この移動も対称に行われるので、移動後もこれらの要素は対称といえます。面a0rb、a1rbは移動後は鏡の面に対して垂直なので、これと先の対称性を満たすのは面a0rb、a1rbが同一の平面である場合のみです。また、a0r1-a0r2、a1r1-a1r2は鏡の面に対して対称なので、鏡の面に対称して回転し、鏡の面に平行になったときに互いに平行になります。
最後に、鏡の面に対して面a0rb、a1rbが平行になるように回転します。これも各要素を同様にそれぞれ一緒に、同時に鏡の面に対して対称に行います。このとき回転方向は鏡の面と面a0rb、a1rbに対して垂直になります。また、a0r1-a0r2、a1r1-a1r2は面a0rb、a1rbならびに鏡の面に対しても平行なので、この回転移動でも平行を保ったままとなります。
a0b1-a0b2は面a0rbと、a1b1-a1b2は面a1rbと平行で、面a0rb、a1rbも平行なのでa0b1-a0b2とa1b1-a1b2は平行またはねじれの関係にあります。また、先と同様に空間的位置関係を保った対称移動であり、a1b1-a1b2はa0b1-a0b2の鏡像なので、a1b1-a1b2とa0b1-a0b2は平行または交わる関係にあります。よって、a0b1-a0b2とa1b1-a1b2はこの両方の条件を満たす平行である、といえます。
ここまでの説明で、「ある物体とその鏡像の任意の二方向をそろえること」が鏡の面に対する対称移動のみでなされることが確認できました。よって、点q0、q1も面a0rb、a1rbとの空間的位置関係を保ったまま対称移動したことになります。当初、これらの要素が鏡の面に対して対称的な位置にあったことから、この移動後も同様に鏡の面に対称的な位置にある、といえます。また、最終的に面a0rb、a1rbは鏡の面と平行になるので、点q0、q1が面a0rb、a1rbと重なるのでなければ、点q0、面a0rbの関係と点q1、面a1rbの関係は鏡の面に対称なので鏡の面(と面a0rb、a1rb)に対して垂直方向については逆になる、といえます。
もう少し詳しく述べるなら、点q0が面a0rbよりも鏡の面のほうにあるなら点q1も面a1rbよりも鏡の面のほうにあり、点q0が面a0rbよりも鏡の面の反対側にあるなら点q1も面a1rbよりも鏡の面の反対側にあります。つまり鏡の面に対して垂直方向について、面a0rbからの点q0の存在する方向と面a1rbからの点q1の存在する方向は逆である、ということになります。また、点q0、q1が面a0rb、a1rbと重なった場合については、面a0rbからの点q0の存在する方向と面a1rbからの点q1の存在する方向は距離0で逆であるといえます。
とここまで書いてみたのですが、もっとエレガントな解き方があるような気がする……こんな説明でなんか悔しい。これも図を見れば一目瞭然とか自明の範疇にはいる事柄なのかもしれませんが、感覚でなく理屈で説明しておきたかったので書いてみました。
●二つの三角形からの結論
ここで三角形p0q0s0と三角形p1q1s1に着目するなら、この二つは合同なので線分q0s0=線分q1s1であり、また線分q0s0と線分q1s1は同じ向きの平面(面a0b0、面a1b1)にともに垂直なので平行となります。よって、点q0と点q1は任意のそろえた二方向に対して垂直に方向が逆になっている、といえます。
物体は点の集合なので、ある一点について証明できれば全体についても同じことがいえます。よって、物体A0と鏡像A1について、任意の互いに平行でない二方向をそろえれば残りのその二方向に垂直な一方向については逆になっている、といえます。これは、鏡像A1はあらゆる一方向において物体A0と逆になりうる、すなわちあらゆる一方向についても物体A0の鏡像になることを意味します。
●物体の一方向が異なる場合の鏡像について
以上は「鏡像の三方向の考察 その1」で述べた鏡像A1と鏡像A2が異なる物体であっても通る理屈を考えたつもりです。しかし、鏡像同士が同じ物体かどうか不明でも「ある物体の鏡像があらゆる一方向においてもその物体の鏡像である」ことから、以下のことが導き出せます。
1. 物体A0のある一方向の鏡像は、一つだけ存在する。
2. その鏡像は、あらゆる一方向においても確かに物体A0の鏡像である。
3. 2.より物体A0の一方向が異なる場合の鏡像、鏡像A1と鏡像A2について、一方をもう一方と同じ角度にしても物体A0の鏡像である。
4. しかし、鏡像A1と鏡像A2が異なるのであれば、物体A0のある一方向の鏡像が複数存在することになる。
5. 4.は1.の前提に反するので、鏡像A1と鏡像A2は同一である、といえる。
こんな話でいいでしょうか。
これで満足できました。私が。ここまで頑張って書いてきましたが、いいんでしょうか。結論はこれでいいと思いますが、数学として思考の経過や記述が正しいか若干不安があります。誤りがあった場合はご容赦のほどお願い致します。
●まとめ 「で、なぜ鏡に左右逆に映るの?」
ここで当初のテーマに接続すると、ある物体とその鏡像について、任意の平行でない二方向をそろえると、その二方向に垂直な一方向がが逆になる性質があります。しかし、我々は最初に説明した通りに、物体の向きを判断するのにまず上下と前後を基準にして考えてしまいがちです。ここで上下前後によって規定される左右はどうしても後回しになってしまいます。地上に立っている鏡に立っている自分自身が映っている状況なら尚更です。よって、鏡は左右(だけ)を逆に映す、と認識するということになります。
更に付け加えるなら、「右目」や「左手」のように、立っているときを基準にした身体の名称が心理的に影響していることも考えられます。つまり「今、自分は左手を上げているが、鏡の中の自分は右手を上げているから逆だ」という考え方がこれで、この状況を「自分も鏡の中の自分も、自分の身体の中心から同じ側の手を上げている」と意識することも可能でしょう。
ところで、少し考えたのですが……以下の状況では、一体どうすればいいんでしょう。
また、上下方向が通常(足が下にあって視線が上下方向に対して垂直な場合)の左右と一致する場合、なんてのもありますよね。
更に我々は、普通にものを見ている場合でもおでこのほうを「上」、あごのほうを「下」と捉えがちな習慣もあるので、なかなか難しい話だな、と思う次第です。
●n次元の物体について
ここで今一度、三次元の物体について、その物体と鏡像の各三方向のうち一方向が逆になった物体について考えてみます。
ここで考えたいことは、鏡像の「逆にした方向(赤)」と「逆にしていない方向(青、緑)から任意の一方向を無視した場合の残りの方向」とで、元の物体と同じようにそろえられるか、そして、無視した任意の一方向は逆になるのか、ということです。
三次元の物体の場合は、「逆にしていない方向から任意の一方向を無視した場合の残りの方向」は一次元で、逆にした方向と合わせて二次元です。逆にした方向(赤)と、残りの方向のいずれか(ここでは緑)とで、元の物体と同じようにそろえられます。
このとき、残りの一方向(青)は逆になります。その結果、三次元の物体の鏡像については、ある一方向(ここでは赤)が逆(で他の二方向が逆でないの)であれば、その方向以外の方向(ここでは青、緑の二方向)のうち任意の一方向(ここでは青)が逆で他の二方向(赤、緑)が元の方向とそろえることができる、ともいえます。そして、「一方向だけ逆で他の二方向はそろえられる」パターンが次元数だけ生じる、というわけです。
さて。今まで三次元の物体について説明してきましたが、ここまできたらn>3のときのn次元の場合についてはどうなるか考えてみたくなるのが人情というものです。
たとえばa(a1, a2, a3, a4, a5, a6, a7)で表される7次元の物体があったとして、a1とa2の二方向だけ逆にした鏡像a12を考えます。このとき、鏡像a12について逆にしていない方向のうち任意の二方向(a3, a4)を除いた残りの方向(a5, a6, a7)と逆にした二方向(a1, a2)の五方向(a1, a2, a5, a6, a7)について元の物体と同様にそろえられるのか、そのとき除かれた二方向(a3, a4)は逆になるのか、あるいはまた、逆にした二方向と逆にしていない五方向から一つずつとった(a1, a6)の二方向を除いた五方向(a2, a3, a4, a5, a7)についても元の物体と同様にそろえることができて、除かれた二方向(a1, a6)は逆になるのか、そういえるのならそれがどのぐらい存在するのか、方向の数だけか、それとも逆にした方向の組み合わせの数だけあるのか、そんなことが気にかかります。これ以上はちょっと私にはわかりかねます。
試しに四次元の物体では?初めはこう考えていました。まず、通常の三次元目に加えてうねうねした線をとりあえず四次元目だと思ってください。四次元の物体のうち一方向(ここでは赤)を逆にしています。
そして、逆にしていない方向(青、緑、うねうね)から任意の一方向(緑)を除いた場合、残りの二方向(青、うねうね)と逆にした方向(赤)とで三方向で、これは下図のようになるのでそろえるのは無理なのではないだろうか、と。
四次元の物体でだめなら五次元以上でもだめだろうから、n次元の物体(n>3)について一方向だけ逆にした鏡像Xについて、逆にしなかった方向のうち一方向除いた方向と逆にした方向とを元の物体を同じようにそろえることはできない、ということになります。つまり、元の物体の鏡に対する向きが変わったら鏡像Xは鏡像ではなくなるのではないか、と。ただ、逆にしなかった方向から逆にした方向を引いて1か0のときなら回転してそろえられそう、とまでは考えてみたのですが。
ただ、別の考え方もあって。まず一次元の対称な物体を考えてみます。
一次元の世界では、対称であっても直線的な移動しかできないのでそろえることはできません。しかし、二次元の世界では新たな方向を利用してくるっと回せばそろえることができます。
次に、二次元の対称な物体を考えてみます。
二次元の世界でも、対称であっても平面的な移動しかできないのでそろえることはできません。しかし、三次元の世界では先と同様に新たな方向を利用してくるっと回してそろえられます。
ということは、先に四次元の物体について「逆にしていない方向から一方向を除いた残りの方向と逆にした方向とを元の物体にそろえることはできない」と書いたのですが、見慣れた三次元の空間に一つ次元を加えたのが実はよろしくない誘導で、おそらく四次元目(?)の方向を利用してそろえることができるのだろうと思います。
●終わりに
先の章で述べたことが数学的にはどうなっているのか、もうとっくに解決された問題なのか、そうでないのか、それとも問題提起とともにすぐ解ける類の問題なのか、正直わかりません。この記事を書くにあたって大学の時の数学の教科書を読んだのですが、宇宙語に近いものを感じました。「可」以上をとったのは確かなのですが、全然内容を覚えてません。でも、こうして書けるだけは書いてみました。座標で点などが表せる以上は計算すれば証明することもできるのだろうなあ、とは思います。
ところで、次元の概念って普通は直線で、どこかから別のどこかへいくものと考えているのですが、どこかから元のどこかへ循環する次元というのもあるのでしょうか。それが先の章の話に絡んできたらどうしよう。
(完)
【宣伝です!】作曲した作品の動画をYoutubeで公開してます!
プリーズチャンネル登録!プリーズチャンネル登録!ニコニコ動画もどうぞ!
今回のアフィリエイトは左右特集です。(いずれも私は未読です。)